Gehirntheorie des Menschen

Das Helligkeitsmodul mit räumlicher Ausbreitung entstand aus dem Helligkeitsmodul mit seitlicher Ausbreitung durch ein Dickenwachstum der Outputschicht - verbunden mit einem Anwachsen der Anzahl der Outputneuronen. Diese waren nun in der Outputschicht räumlich verteilt. So kam neben der x-Koordinate und der y-Koordinate noch die z-Koordinate für die Höhe eines Neurons in dieser Schicht hinzu.

Wir sollten bedenken, dass das Dickenwachstum bei vielen Wirbeltieren wahrscheinlich zuerst auftrat, während später das seitliche Wachstum einsetzte.

Wir haben in dieser Monografie die Folgen des Dickenwachstums zuerst beschrieben und bei den Orientierungssäulen dieses Dickenwachstum zunächst ausgeblendet. Sonst wäre der mathematische Apparat völlig undurchsichtig geworden. Nun jedoch erweitern wir das Konzept des vorangegangenen Kapitels um das Dickenwachstum. Zusätzlich verarbeiten wir im erweiterten Modul die Helligkeiten.

Damit benötigen wir anstelle der bisherigen vier Inputneuronen nunmehr acht. Vier Inputneuronen von magnocellularen Ganglienzellen liefern den Dunkel-On-Input in die Schicht 4-Dunkel-On. Über ihr befindet sich die Schicht 3-Dunkel-On. Darüber befindet sich die Schicht 4-Hell-On. Dort treffen die Signale der vier Ganglienzellen vom Hell-On-Typ ein.

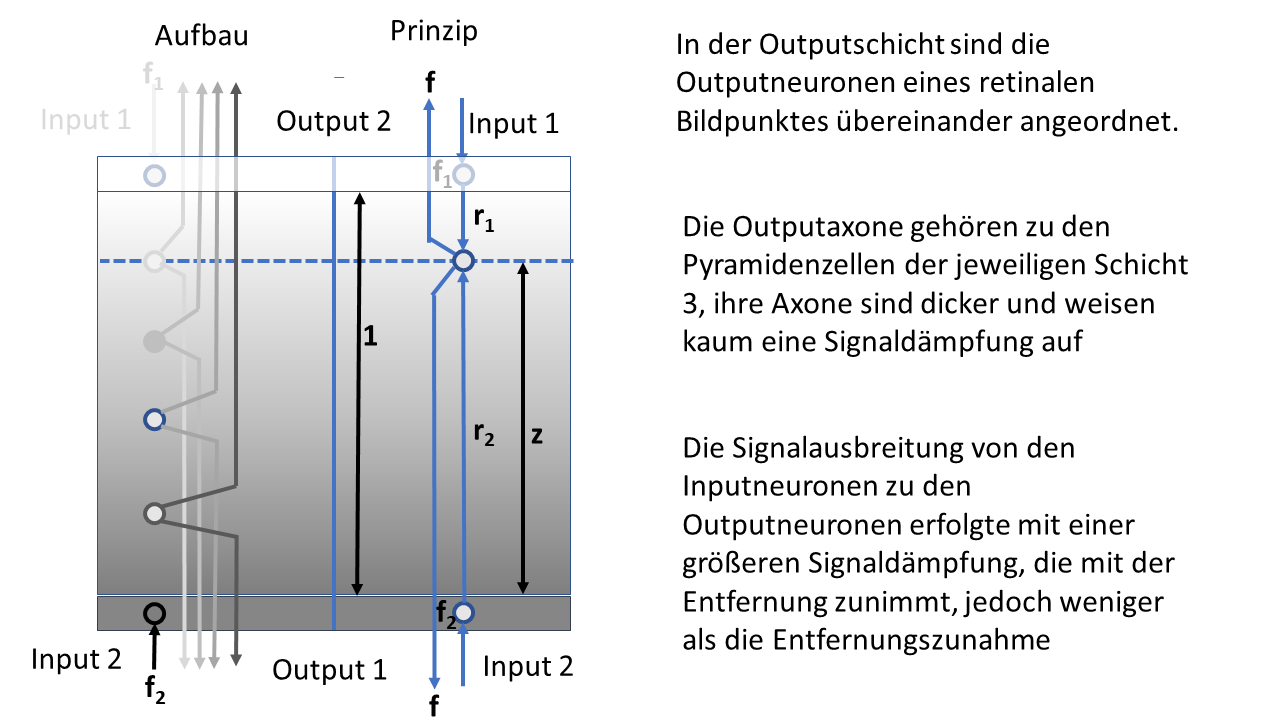
Abbildung 28: Helligkeitsmodul mit räumlicher Signalausbreitung

In der obigen Abbildung ist das Modul im Querschnitt zu sehen, seine seitliche Ausdehnung ist hier nicht dargestellt. Wichtig für die späteren Betrachtungen ist die Höhe z des Outputneurons, dessen Erregung wir berechnen werden.

Im Kapitel über das Helligkeitsmodul mit seitlicher Signalausbreitung hatten wir die Feuerrate einer magnocellularen Ganglienzelle mit der Sehnenlänge s in Verbindung gebracht. Eine dunkle, geneigte Gerade mir einem Anstellwinkel α schneidet den Kreis, der vom rezeptiven Feld der Ganglienzelle gebildet wird und führt dort zur Abdunklung. Die Ganglienzelle von Dunkel-On-Typ reagiert auf diese Verdunklung mit der Zunahme der Feuerrate. Wir gingen davon aus, dass die Feuerrate gleich dem Quadrat der Sehnenlänge sein. Ein eventueller Proportionalitätsfaktor fällt beim Differenzieren heraus.

Wir ordnen den Kreis in der x-y-Ebene so an, wie es die nachfolgende Abbildung zeigt.

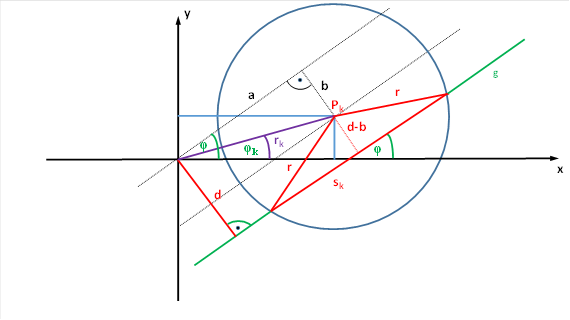
Abbildung 29: Berechnung der Sehnenlänge für ein rezeptives Feld einer Ganglienzelle

Dann ergibt sich für die das Quadrat der Sehnenlänge s_k die Gleichung

Dies wurde im Kapitel 4.2.3. bereits bewiesen.

Wir untersuchen nun die Sehnenlängenquadrate für vier retinale Ganglienzellen in der folgenden Anordnung, die bereits im Kapitel 4.2.4. verwendet wurde.

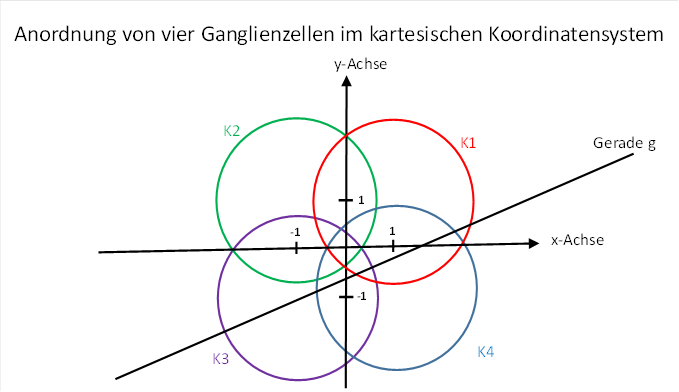
Abbildung 30: Anordnung von vier Ganglienzellen im kartesischen Koordinatensystem

Für die Quadrate der Sehnenlängen, die letztlich als Feuerrate der Ganglienzellen verwendet werden, gelten (wie in 4.2.2. hergeleitet) die Formeln

Wir können die Ausdrücke in den Winkelfunktionen vereinfachen. Weil nach unserer Annahme die Feuerrate jeder Ganglienzelle mit dem Quadrat der Sehnenlänge übereinstimmt, gelten für die vier Feuerraten folgende Gleichungen:

Zur Erinnerung: r ist der Radius der rezeptiven Felder der vier magnocellularen Ganglienzellen, also der vier Kreise, die von der Geraden g geschnitten werden.

Diese Formeln für die Feuerrate gelten, wenn eine schwarze Linie vor weißem Hintergrund die rezeptiven Felder der vier beteiligten Ganglienzellen vom Dunkel-On-Typ schneidet.

In einem System, bei dem die magnocellularen Ganglienzellen auch Helligkeiten bewerten können, wird die Feuerrate bei einer schwarzen Geraden genau die Werte der quadrierten Sehnenlänge annehmen.

Ist jedoch die Gerade nicht schwarz, sondern grau, wird die Ganglienzelle (vom Dunkel-On-Typ) weniger erregt sein. Es wird ein Korrekturfaktor nötig sein, der bei zunehmender Helligkeit des Grauwertes der Geraden die Feuerrate vermindert, so dass sie weniger als das Sehnenlängenquadrat wird. Wir entscheiden uns für einen exponentiellen Ansatz, der sich bereits beim motorischen Divergenzmodul bewährt hat.

Es sei h eine Größe aus dem Intervall <-1,+1>. Wir wollen h als die relative Helligkeit bezeichnen - man kann sie als positive oder negative Prozentzahl interpretieren. So entspricht Weiß der Helligkeit 1, Schwarz der Helligkeit -1.

Ist f_s die Feuerrate einer Dunkel-On-Ganglienzelle bei einem schwarzen Objekt im rezeptiven Feld dieser Zelle und f(h) die Feuerrate, wenn das Objekt nicht schwarz ist, sondern den Grauwert h besitzt, so soll folgendes gelten:

Wir müssen nun in den vier Feuerraten unserer Ganglienzellen die relative Helligkeit u der Linie berücksichtigen, die die rezeptiven Felder schneidet. So erhalten wir die Formeln

Damit wir künftig die Feuerraten der Dunkel-On-Ganglienzellen und der Hell-On-Ganglienzellen unterscheiden können, wählen wir für die obigen Dunkel-On-Ganglienzellen den Index D, er soll das Wort Dunkel repräsentieren. Dann gilt für unsere vier Feuerraten:

Die Feuerraten der Hell-On-Ganglienzellen genügen, wenn eine helle Linie mit der Helligkeit h (dem Grauwert h) vor schwarzem Hintergrund erscheint, den Formeln

Somit haben wir nun die Feuerraten von vier Ganglienzellen des Typs Dunkel-On und vier vom Typ Hell-On sowie die zugehörigen Feuerraten. Von diese acht Ganglienzellen projizieren nun vier in die magnocellularen Subschicht 4-Dunkel-On, die restlichen vier in die Schicht 4-Hell-On.

Die topologische Anordnung sei vorgegeben. Wir haben insgesamt vier benachbarte Augendominanzsäulen aus dem gleichen Auge. Dadurch entsteht ein Würfel. Seine vier oberen Ecken erhalten die retinalen Hell-On-Input. Die unteren Ecken empfangen den Dunkel-On-Input.

Jede einzelne Feuerrate ist bei einer Dunkel-On-Ganglienzelle mit dem Korrekturfaktor für die Helligkeit h zu versehen, wenn die Linie nicht die Farbe Schwarz hat, sondern die relative Helligkeit h. Gleiches trifft für die Hell-On-Ganglienzellen zu. Diese Korrekturfaktoren haben wir in die acht Feuerraten bereits eingearbeitet.

Wir betrachten zunächst die vier Dunkel-On-Inputneuronen. Sie mögen genau so angeordnet sein wie im vorigen Kapitel.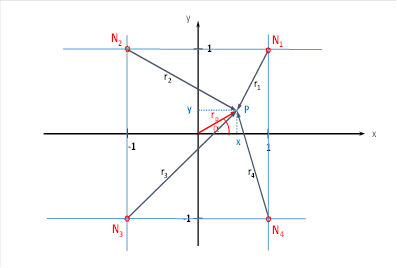

Abbildung 31: Vier cortikale Outputneuronen im Helligkeitsmodul mit räumlicher Signalausbreitung

Für die Feuerrate des Neurons im Punkt P hatten wir bereits eine Formel hergeleitet:

Sie ergibt sich so, weil eine abstandsabhängige Dämpfung auftritt, die mit dem Quadrat der zurückgelegten Entfernung exponentiell zunimmt. Dadurch wird die Feuerrate mit dem Quadrat der Entfernung exponentiell abnehmen, daher der negative Exponent in der e-Funktion.

Nun müssen wir bedenken, dass das Divergenzmodul räumlich ist. Neben der Breite x und der Länge y gibt es für jedes Neuron der Schicht S3-Dunkel-On eine Höhe z.

Wir betrachten dasjenige Outputneuron, welches die bereits bekannten Koordinaten x und y in der Breite und Länge besitzt, und das gleichzeitig die Höhe z hat. Dazu klappen wir die x-y-Ebene aus der Abbildung in die Waagerechte. Dann befindet sich das Outputneuron im Punkt P(x,y,z) genau senkrecht über den Punkt P der obigen Abbildung.

Wenn wir den Punkt P(x,y,z) mit den unteren Ecken des Würfels verbinden, also mit N₁ bis N₄, erhalten wir vier neue Vektoren t₁ bis t₄. Sie verbinden den Punkt P(x,y,z) mit den unteren Würfelecken und geben die Länge der Strecke an, die die neuronale Erregung von den Würfelecken bis zum Punkt P(x,y,z) zurücklegen muss.

Dann ist die von den vier unteren Ecken eintreffende Erregung f_u im Punkt p(x, y, z) gleich

In der Skizze sieht man die Veränderung, wenn die Erregung von den vier Outputneuronen sich räumlich ausbreitet und den Punkt P(x,y,z) erreicht, dessen Höhe über der x-y-Ebene gleich Z ist.

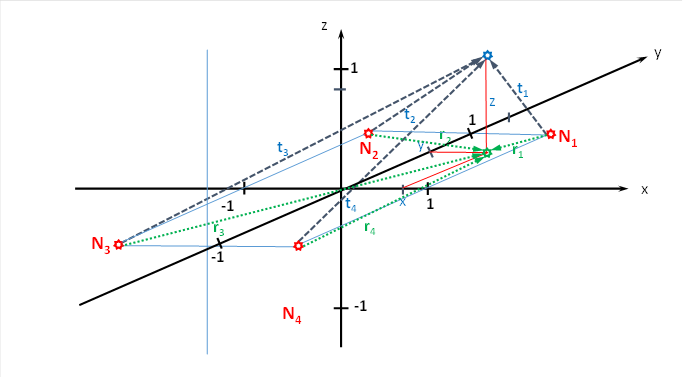
Abbildung 32: Herleitung der Länge der Radiusvektoren für das Helligkeitsmodul mit räumlicher Signalausbreitung

 

Vom Neuron N₁ (rot dargestellt) verläuft der neue Radiusvektor t₁ zum Outputneuron (blau) mit der Höhe z (rot). Er bildet die Hypotenuse eines rechtwinkligen Dreiecks, dessen Katheten von r₁ und z gebildet werden. Nach Pythagoras gilt daher

Für die anderen drei neuen Radiusvektoren gilt analog

Wir können diese neuen Radiusvektoren in unsere Formel für das Outputneuron einsetzen.

Den in allen vier Summanden vorkommenden gemeinsamen Bestandteil können wir ausklammern und als Faktor vor die Summe ziehen.

Dies ist die Formel für die Erregung, die das Outputneuron P(x,y,z) von den vier unteren Inputneuronen empfängt. Die Erregung ergibt sich bei räumlicher Erregungsausbreitung dadurch, dass wir die Erregung für die Ausbreitung in der x-y-Ebene wählen und mit dem Faktor  multiplizieren.

Wir ändern nun im Nachhinein die Bezeichnungen für die vier Inputerregungen f₁ bis f₄. Der Grund ist einfach: Es handelt sich um den Input der vier Dunkel-On-Neuronen aus der Retina. Daher ersetzen wir das Symbol f durch das Symbol f_D.

Die Feuerraten f_D = f_D(h) ergeben sich durch Multiplikation mit dem Korrekturfaktor e^-u, diesen können wir als Proportionalitätsfaktor vor die Summe schreiben. Daher gilt

Diesen Erregungsbeitrag leisten die unteren vier Dunkel-On-Neuronen, wenn die geneigte Gerade, die ihre rezeptiven Felder schneidet, die Helligkeit u hat.

Dieser Erregungsanteil besteht aus zwei Faktoren.

Der erste Faktor berücksichtigt den Abstand z des Outputneurons im Punkt P(y,x,z) von der x-y-Ebene sowie die Helligkeit der Geraden, welche die rezeptiven Felder der vier On-Typ-Neuronen der Retina schneidet.

Der zweite Faktor

ist genau die Feuerrate des Helligkeitsmoduls mit seitlicher Signalausbreitung vom Dunkel-On-Typ, die wir bereits im Kapitel 4.2.2. hergeleitet haben.

Nun müssen wir berücksichtigen, dass unser Outputneuron nicht nur Input aus den unteren Ecken des Würfels mit der Kantenlänge 1 empfängt, sondern auch von den vier oberen Ecken.

Hier beträgt der Abstand des Outputneurons (blau) zur oberen Würfelfläche jedoch genau 1-z, denn unser Würfel sollte die Kantenlänge 1 besitzen.

Daher wird unsere Formel für den Input von oben dadurch gewonnen, dass wir in der Formel für f_D den Abstand z durch den neuen Abstand 1-z ersetzen und statt f_D nun f_H verwenden. Denn die oberen vier oberen Neuronen empfangen von der Retina die Hell-ON-Signale derjenigen magnocellularen Ganglienzellen, die zu unseren vier Retinapunkten gehören. Jeder Retinapunkt verfügt über ein Dunkel-On-Signal und über ein Hell-On-Signal.

Damit empfängt unser Outputneuron von den oberen vier Neuronen folgende Erregung:

Der Einfluss der Signalausbreitung in der z-Richtung (Signaldämpfung) wird durch den ersten Faktor berücksichtigt, der Beitrag der Signaldämpfung in der x-y-Ebene durch die Radiusvektoren r₁ bis r_k.

Die Hell-On-Ganglienzellen empfangen in unserem erweiterten Modell jedoch nicht die Helligkeit einer weißen Geraden vor schwarzem Hintergrund, sondern einer Geraden mit der Helligkeit u. Daher müssen wir bei allen Feuerraten den Korrekturfaktor e^+u für die Helligkeit berücksichtigen.

Hier wird Einfluss der Signalausbreitung in der z-Richtung (Signaldämpfung) durch den ersten Faktor berücksichtigt, der Beitrag der Signaldämpfung in der x-y-Ebene durch die Radiusvektoren r₁ bis r_k.

Auch dieser Erregungsanteil besteht aus zwei Faktoren:

Der zweite Erregungsanteil

stimmt wieder genau mit der Feuerrate des Helligkeitsmoduls mit seitlicher Signalausbreitung vom Dunkel-On-Typ, die wir bereits im Kapitel 4.2.2. hergeleitet haben. Der Einfluss der Helligkeit wird durch u bewirkt, der Hell-On-Typ wird durch das positive Vorzeichen der Helligkeit bewirkt. Hier hatte der Off-Typ ein negatives Vorzeichen.

Wir bedenken, dass das Outputneuron sowohl den Beitrag der unteren Inputneuronen empfängt, aber ebenso den Beitrag der oberen Inputneuronen. Seine Gesamterregung besteht daher aus einer Summe.

Einsetzen der zwei Teilerregungen ergibt die endgültige Feuerrate des Outputneurons im räumlichen Divergenzmodul.

Hierbei gilt

 

Wir fassen die ersten zwei Faktoren zu einer neuen Funktion zusammen, die wir als Höhenfunktion H des visuellen Divergenzmoduls mit räumlicher Signalüberlagerung bezeichnen.

Dann können wir die Erregung eines beliebigen Outputneurons innerhalb des von uns betrachteten Würfels als Funktionenprodukt schreiben.

Die Funktion f(x,y) ist die Erregungsfunktion, die uns im visuellen Divergenzgitter mit seitlicher Signalausbreitung im Fall des magnocellularen Inputs begegnet ist.

Wir fragen nun nach dem Ort desjenigen Outputneurons im betrachteten Würfel, welches die stärkste Erregung aufweist.

Die strikte Konkavität der Erregungsausbreitung für ein einzelnes Neuron innerhalb einer konvexen Umgebung, in der die Hessematrix negativ definit ist, garantiert, dass die Überlagerung von mehreren Erregungen verschiedener Outputneuronen innerhalb der Überlagerung dieser Umgebungen zu einem globalen Maximum führt.

Zur Berechnung muss im Falle der räumlichen Signalausbreitung die partielle Ableitung nach x, nach y und zusätzlich nach z gebildet und gleich Null gesetzt werden.

Hier erweist es sich als ungeheurer Vorteil, dass die Erregungsfunktion f aus den zwei Faktoren H(z,u) und E(x,y) besteht. Der erste Faktor enthält nur die Variablen z und u. Die Variable u steht für die aktuelle Helligkeit und kann als vorläufige Konstante betrachtet werden. Die Variable z gibt die Höhe eines Outputneurons im Würfel an.

Der zweite Faktor ist eine Funktion, die nur von x und y abhängt und die identisch ist mit der Erregungsfunktion des Helligkeitsmoduls mit seitlicher Signalausbreitung. Hier haben wir die Ableitungen nach x und y bereits berechnet und Null gesetzt. So haben wir die Formeln für den Anstiegswinkel und den Nullpunktabstand einer geneigten Geraden hergeleitet. Genau diese Bedingungen für die x-Koordinate und die y-Koordinate und die Anforderungen an den zugehörigen Phasenwinkel und den Radiusvektor in der x-y-Ebene gelten auch im Modul mit räumlicher Ausbreitung.

Die Höhenkoordinate des Maximumneurons wird von der Funktion H(z,u) vorgegeben. Hier bestimmt die Helligkeit u die Höhenkoordinate z.

Dies muss durch Bildung und Nullsetzung der Ableitung der Funktion H(z,u) nach z ermittelt werden. Die Funktion E(x,y) tritt in der Erregungsfunktion als konstanter Faktor auf, weil diese Funktion die Variable z überhaupt nicht enthält. Der konstante Faktor wird beim Nullsetzen herausdividiert und fällt daher heraus.

Wir müssen also nur noch die Ableitung der Funktion H(z,u) nach z berechnen und gleich Null setzen, um die Höhe z des Maximumneurons im Würfel zu ermitteln.

Wir berechnen die Ableitung:

Umformen ergibt

 

 

 

Mit dieser Gleichung können wir ermitteln, welchen Helligkeitswert u die Gerade besitzen muss, damit das Neuron mit der Höhe z innerhalb des Würfels die maximale Erregung unter allen Neuronen dieses Würfels erreicht.

Dieses Neurons ist unter allen Neuronen im Würfel am stärksten erregt, wenn der Anstellwinkel φ der geneigten Geraden im Sichtfeld der Bedingung genügt,

die wir bereits für das Helligkeitsmodul mit seitlicher Signalübertragung hergeleitet hatten:

 

Wenn sich die Helligkeit der Geraden verändert, ohne dass sie ihren Winkel und ihre Position verändert, dann verändert sich nur die Höhe z des maximal erregten Neurons, während die Koordinaten x und y unverändert bleiben.

Mit dem Dickenwachstum der magnocellularen Outputschicht der Klasse 3 des Cortex entstand wiederum eine neue Modalität: Helligkeitswert von Linienelementen.

Waren in der nur einlagigen Neuronenschicht ausschließlich schwarze oder weiße Linienelemente hinsichtlich ihres Orientierungswinkels analysierbar, so konnte die neue Modalität die Helligkeit dieser Linienelemente nach Graustufen detektieren. Weil sich neue Modalitäten im Verlauf der Evolution aufspalten und eigene, separate sekundäre Cortexgebiete ansteuern, entstanden im sekundären visuellen Cortex nun so viele Retinaabbildungen, wie es Graustufen gab. Da aber jede Retinaabbildung bereits in separate Abbildungen für die verschiedenen Winkelbereiche aufgeschlüsselt war, gab es für die Kombination einer jeden Graustufe mit jedem detektierbaren Winkelintervall ein eigenes, separates Retinaabbild.

Bei 20 Graustufen und 30 Winkelintervallen gab es also insgesamt 600 Retinaabbildungen im sekundären Cortex. Diese waren nicht wild durcheinandergemischt. Marker sorgten dafür, dass beispielsweise in Längsrichtung die Retinaabbilder nach aufsteigenden Orientierungsrichtungen der Linienelemente sortiert waren, während in der Breite die Sortierung nach ansteigenden Helligkeitswerten (Grautonsortierung) erfolgte.

Dies erscheint mir sehr real, denn so konnte in jedem Retinaabbild auf auftauchende Signale reagiert werden. Ein Schwerpunktmodul für jede dieser vielen Retinaabbildungen errechnete der Ort des Signalmittelwertes und sandte Signale an die Augenmuskeln, die eine Zentrierung auf den Signalschwerpunkt bewirkten.

Da von den unzähligen Retinaabbildungen jedoch immer nur sehr wenige aktiv waren (eine Linie konnte auf einem Retinapunkt prinzipiell nur einen Winkelwert erzeugen - kreuzende Linien maximal zwei,-), verlagerte sich die neuronale Aktivität ständig von einer Retinaabbildung zur nächsten, wenn sich etwas veränderte. Daher wandern Aktivitätszentren im sekundären visuellen Cortex hin und her, wenn man z. B. einen Film anschaut.

Wichtige Bemerkung:

Als Autor habe ich in dieser Monografie einige grundlegende Annahmen gemacht. So beispielsweise die Annahme, die Erregung eines Neurons breite sich im räumlichen Divergenzgittern gemäß der Formel

aus, wobei f(0,0,0) die Feuerrate im Koordinatenursprung sei, wo sich auch das Inputneuron befindet. Das Outputneuron dagegen sei im Punkt P(x,y,z) angeordnet und habe vom Koordinatenursprung den Abstand r. Als Physiker wäre mir die Formel

viel lieber gewesen. Aber der von mir gewählte Ansatz sichert, dass die Erregung eines Neurons in einem Würfel, der seinen Input an den acht Ecken bezieht, von denen die unteren Neuronen das inverse Signal der oberen erhalten, immer zur Bildung von Orientierungssäulen führt, wenn im rezeptiven Feld eine geneigte Gerade auftaucht. Hierbei kann man den Würfel in kleine waagerechte Scheiben schneiden und stellt folgendes verwundert fest:

In jeder der waagerechten Scheiben gibt es genau ein Erregungsmaximum. Solange der Anstellwinkel und die Position der Geraden unverändert bleiben, liegen die Orte mit der maximalen Erregung in jeder dieser dünnen Scheiben genau übereinander.

Jeder Neurologe, der in einen solchen Neuronenwürfel mit einer feinen Messsonde senkrecht hineinsticht, wird (wenn er ein Neuron erwischt) ein neuronales Signal erhalten. Wenn er eine geneigte Gerade durch das Bildfeld parallel zu sich selbst verschiebt, so wird dieses Neuron bei einer bestimmten Position der Gerade maximal feuern, wenn diese Gerade den für dieses Neuron günstigsten Einstellwinkel besitzt. Man muss also geduldig den Anstellwinkel und die Position der Geraden solange verändern, bis dieses eine Neuron maximal feuert.

Bewegt man die feine Messsonde nun tiefer, so zapft man eine tiefer gelegene Schicht des Würfels an. Erstaunlicherweise ist das dortige Neuron ebenfalls maximal erregt, denn die Nachbarneuronen auf gleicher Höhe feuern weniger stark. Deshalb prägte man den Begriff Orientierungssäule. Alle Neuronen in der Säule sind bei einem bestimmten, für diese Säule charakteristischen Anstellwinkel sehr stark erregt, aber immer nur eines unter ihnen am stärksten.

Wäre in der Übertragungsfunktion f(x,y,z) von mir anstelle der zweiten Potenz des Abstandes die dritte Potenz verwendet worden, so wären die Erregungsmaxima in den verschieden hohen Schichten des Neuronenwürfels nicht mehr genau übereinander angeordnet gewesen. Das Differential der Funktion wäre nicht in zwei Faktoren zerlegbar, von denen der eine nur die Koordinaten x und y der Ebene besitzt, während der zweite Faktor nur die Höhenkoordinate z beinhaltet. Nur dann besitzt die Erregung in einer zur x-y-Achse parallelen Fläche ihr globales Maximum immer an der gleichen Stelle, wenn der Anstellwinkel der Geraden und ihre Position konstant sind.

Diese experimentell bestätigte Erkenntnis bewog mich, zu dem mathematischen Ansatz, die Dämpfung von neuronalen Erregungen bei der Ausbreitung im Raum mit der zweiten Potenz des Abstandes von der Erregungsquelle anzusetzen. Es war also keine Willkür, um einfachere Formeln zu gewinnen, sondern der Wunsch, die Formeln zu wählen, die zu experimentell bewiesenen Fakten passen. Die Realität sollte der Maßstab für die Wahl der neuronalen Übertragungsfunktion sein.

Den messenden Neurologen kann nun ein neuer Messauftrag erteilt werden: Weisen Sie durch Messung nach, dass die Erregung innerhalb der gleichen Orientierungssäule von der Höhe abhängt und die Höhe z im magnocellularen Teil der Säule die Helligkeit der Geraden (ihren Grauton) verschlüsselt. Zu jedem Grauton der Geraden ist in dieser Säule genau ein Neuron maximal erregt. Seine Höhe hängt direkt von dem Grauwert der Geraden ab.

In dem parvocellularen Teil der Säule ist folgendes zu beweisen: Innerhalb einer Orientierungssäule, die einem Anstellwinkel und einer Position der Geraden im Blickfeld zugeordnet ist, hängt die Höhe des maximal erregten Neurons von der Farbe der Linie ab. Jede Farbe ist eindeutig der Tiefe des Einstichs mit der Sonde zugeordnet.

Die Orientierungssäule kann in Farbschichten unterteilt werden derart, dass diese waagerecht angeordnet sind. Die von den Neuronen dieser Schicht detektierte Farbe ist in der gesamten waagerechten Schicht identisch. Die Neuronenhöhe in der parvocellularen Cortexschicht V1 ist genau einer Farbe zugeordnet, solange man sich innerhalb des Farbmoduls bewegt.

Und weil die Position einer Farbe in der Höhe über die erste Ableitung ermittelt wurde, gilt das Gesetz der Farbkonstanz. Konstante Faktoren wie etwa die Helligkeit fallen beim Differenzieren unter den Tisch, ihr Einfluss verschwindet völlig.

 

1.   

2.   

3.   

4.   

4.1.   

4.2.   

4.3.   

4.3.1.   

4.3.2.  Das Farbmodul mit räumlicher Signalausbreitung

 

Nach der Erklärung des Helligkeitsmoduls mit räumlicher Signalausbreitung ist es an der Zeit, das Modulkonzept auf die Probe zu stellen.

Behauptet wurde von mir, dass ein Wechsel der Modalität keinen Einfluss auf die Arbeit eines Gehirnmoduls hat. Wir werden dies nun zeigen.

Ersetzt man im Helligkeitsmodul mit räumlicher Ausbreitung den magnocellularen visuellen Input durch den parvocellularen, so bleiben alle Formel erhalten. Die Feuerraten geben hier nicht mehr die Erkennung einer Geraden mit einer vorgegebenen Graustufe wieder, sondern die Graustufe wird durch die Farbsättigung ersetzt. Die Hell-On-Ganglienzelle reagiert nun im Rot/Grün-Modul auf rotes Licht. Sie ist vom On-Typ. Je stärker der Rotanteil des Lichtes ist - und Licht ist meist eine Farbmischung - umso stärker feuert das Rot-On-Neuron. Von grünen Lichtanteilen wird es dagegen gehemmt.

Die Dunkel-On-Ganglienzelle wird von der Grün-On-Ganglienzelle ersetzt. Sie feuert umso stärker, je höher der Grünanteil des Lichtes ist.

Es sei u wieder eine relative Größe, die den relativen Rotanteil im Verhältnis zum Grünanteil bewertet und Werte von -1 bis +1 annehmen kann. Der Wert u = 1 entspricht dem Farbwert Rot, der Wert -1 dem Farbwert Grün. Der Wert u = 0 entspricht dann nach den Gesetzen der Farbmischung dem Farbwert Gelb.

Ist f_H die Feuerrate der Rot-On-Ganglienzelle und f_D die Feuerrate der Grün-On-Ganglienzelle, die ja gleichzeitig eine Rot-Off-Ganglienzelle ist, so mögen folgende Gleichungen gelten:

Damit unterscheidet sich der Input nicht wesentlich vom Input in das Helligkeitsmodul mit räumlicher Übertragung.

Wenn nun eine Gerade mit dem Farbwert u > 0 im rezeptiven Feld der Ganglienzelle erscheint, während der Hintergrund die Komplementärfarbe aufweist (worauf die Ganglienzelle fast gar nicht reagiert), so wächst die Feuerrate wieder quadratisch mit der Sehnenlänge. Genauso war es im Helligkeitsmodul.

Daher unterscheidet sich das Outputverhalten der Neuronen eines Würfels, dessen untere Ecken den On-Input der grünempfindlichen und im Quadrat angeordneten Retina-Ganglienzellen empfängt, und dessen obere Ecken den zugeordneten Retinainput von den rotempfindlichen Ganglienzellen der gleichen Retinapunkte empfangen, mathematisch in keiner Weise vom Helligkeitsmodul mit räumlicher Signalausbreitung.

Anstelle des Hell-On-Input tritt der Rot-On-Input. Die Stelle des Dunkel-On-Inputs wird vom Grün-On-Input übernommen.

Und da wir inzwischen wissen, dass der Rot-Grün-Input im Cortex die parvocellularen Schichten S4-Grün und S4-Rot erreicht, zwischen denen die Outputschicht S4-Grün liegt, deren Neuronen jedoch sowohl den Grün-Input von der unteren Inputschicht als auch den Rot-Input der oberen Schicht empfangen können, breitet sich die Erregung von diesen zwei Arten von Farbrezeptoren in der Schicht S3-Grün aus und überlagert sich. Denn insgesamt 8 Inputneuronen liefern ihre Signale zu diesem Würfel. Für ihn gelten genau die gleichen physikalischen und mathematischen Gesetze wie für das Hell-Dunkel-Modul.

Daher gibt es im Grün-Rot-Modul mit räumlicher Signalausbreitung wieder Orientierungssäulen. Diese reagieren nach den gleichen Formeln auf den Neigungswinkel einer Geraden. Und da die Neuronen sowohl im Hell-Dunkel-Modul als auch im Grün-Rot-Modul retinotop angeordnet sind, liegen Inputneuronen ein und derselben Retinastelle in der visuellen Cortexrinde auch genau übereinander. Daher wird eine Orientierungssäule Rot/Grün, wenn sie maximal erregt ist, den gleichen Winkel φ und den gleichen Nullpunktanstand d benötigen wie die Orientierungssäule des Hell/Dunkel-Moduls.

Und für die Farbkombinationen Blau-Grün sowie Rot-Blau gilt das Gleiche.

Die Maximalerregung bei einem vorgegebenem Winkel φ und einem Nullpunktabstand d der geneigten Geraden ist in allen visuellen Modulen der primären visuellen Cortexrinde, egal in welchem Schichtsystem, nur von der x-Koordinate und der y-Koordinate abhängig. Die Modulwürfel für Helligkeit und Farben sind einfach übereinandergestapelt. Daher geht eine Orientierungssäule komplett von der obersten bis zur untersten Schicht hindurch und besteht aus einem oberen Viertel für die Farbmischung Blau-Rot, darunter ein Viertel für die Farbmischung Grün-Rot, wieder darunter ein Viertel für die Farbmischung Rot-Blau und ganz unten ein Viertel für das Modul Hell-Dunkel. Die x-y-Koordinaten der meisterregten Neuronen in diesem Neuronenquader bestimmen den Anstiegswinkel und den Nullpunktabstand einer geneigten Geraden, die Höhe dagegen die Farbe und die Helligkeit. In jedem der vier Module gibt es - falls ein visueller Reiz angeboten wird, je genau ein maximal erregtes Neuron. Aber auch die übrigen Neuronen des Quaders sind erregt, das meisterregte Neuron in einem Modul bildet jedoch den Erregungsmittelpunkt.

Verlässt der Output die Überlagerungsschicht, so tritt eine laterale Nachbarhemmung auf und unterdrückt die schwächeren Signale, so dass sich die Neuronen mit der größten Feuerrate durchsetzen. Ihr Output erreicht weitere Gehirngebiete.

Da die Retina mittels vieler Tausend oder Hunderttausend Ganglienzellen verschiedener Modalitäten (Hell/Dunkel, Farbe-On/Farbe-Off in den primären visuellen Cortex projiziert, bildet er (beim Menschen) ein Signalabbild der visuellen Umwelt in den vier visuellen Submodalitäten. Punkte gleicher Farbe liegen auf gleicher Höhe, die dortigen Neuronen feuern, wenn diese Farbe erkannt wird - jedoch nur, wenn Linienelemente die geforderte Richtungseigenschaft haben.

Gibt es keine geneigten Geraden, also keine Konturen, weil eine Fläche von gleicher Helligkeit oder gleicher Farbe vorhanden ist, so feuern in diesem Falle in den Modulen diejenigen Neuronen, die im zugehörigen Würfel bzw. Quader die x-y-Koordinaten Null haben. Feuern Neuronen mit den Koordinaten x = 0 und y = 0, so gibt es keine Linie in den rezeptiven Feldern der signalliefernden Retinazellen. Dann werden einfach farbige Flächen wahrgenommen und deren Helligkeit ermittelt. Dieser Signalweg dient der Objektanalyse, während die übrigen Orientierungssäulen die Richtungen von Linienelementen verschiedenster Farben analysierten. Weil sie verschiedene Modalitäten darstellten, trennten sich ihre Wege im sekundären Cortex. Und als die Signale den Weg zum dopaminergen Mittelwertzentrum fanden, welches immer alle Signale berücksichtigen musste, war der Weg für eine Bewegungserkennung vorbereitet. Auf dem langen Weg vom ersten, cortikalen Segment zur dopaminergen Substantia nigra im siebenten Segment mussten die visuellen Signale eine Zeitverzögerung erleiden und wurden zu Vergangenheitssignalen. Nun standen dem Gehirn die Gegenwart und die (kürzliche) Vergangenheit in Signalform zu Verfügung. Die Rückprojektion des dopaminergen Mittelwertkerns zum Cortex wies also eine Zeitverzögerung auf. Diese Signalart war eine neue Modalität: die Vergangenheit. Diese lag nur wenige Millisekunden zurück, konnte jedoch in einem neuen Modul zur Bewegungserkennung genutzt werden. Dieses neue Modul waren die Basalganglien. Ihnen ist das nächste Kapitel gewidmet.

Wer die Arbeitsweise der Überlagerungsmodule mit räumlicher Signalausbreitung verstanden hat, der weiß, wie der primäre Cortex prinzipiell arbeitet. Hierbei ist es egal, ob die Modalität eine visuelle, eine motorische, eine taktile, eine Schmerzmodalität, eine elektrosensorische, eine Seitenlinienmodalität oder irgendeine andere Modalität ist.

Dennoch gibt es für alle diesen Modulen eine nachgeschaltete Signalweiterverarbeitung, deren Resultat zurückwirkt auf diese primären Cortexgebiete. Erst dadurch ist es möglich, dass Neuronen in den primären sensorischen Gebieten auch auf Bewegungen reagieren können. Bewerkstelligt wird diese Reaktion durch eine nachgeschaltete Signalverarbeitung in Verzögerungsmodulen. Diese befinden sich im Gehirn der Wirbeltiere im Basalgangliensystem.

An dieser Stelle möchte ich dankbar darauf hinweisen, dass ich sämtliche Kenntnisse über die Basalganglien und deren cytoarchitektonischen Aufbau Herrn Prof. Dr. Rolf Kötter verdanke. Er selbst war ein Schüler von Prof. Karl Zilles, dessen wunderbare Werke mir einen leichtverständlichen Zugang zum Nervensystem des Menschen ermöglichten. Besonders seine sehr ausführlichen Beschreibungen und Abbildungen der verschiedensten Signalwege im Gehirn verliehen mir die Fähigkeit, mir das menschliche Gehirn in all seinen Substrukturen im Geiste vorzustellen und es zu analysieren. Die Arbeiten seiner Doktoranden waren für mich immer eine Fundgrube für neue Erkenntnisse. Ergänzend hierzu verdanke ich Herrn Prof. Gerhard Roth die Einsichten über die Entwicklung des Gehirns während der viele Jahrmillionen andauernden Evolution, die einst bei einfachen Zellhaufen begann.

• ← 4.2.  Divergenzmodule mit seitlicher Signalausbreitung
• 4.4.  Das Disparitätsmodul →